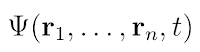1. Solve quantum gravity.
2. Crack RSA (factoring) or prove it impossible (polynomial time).
3. Build a working quantum computer (capable of factoring RSA) or prove it impossible (a separate question from the possibility of classical factoring).
4. Learn to play piano (I can a bit, but learn it well).
5. Build my own CPU from transistor level up.
6. Build my own compiler.
7. Build my own operating system.
8. Build my own AI that rivals humans in general creative tasks.
9. Build my own house.
10. Build my own car.
11. Acquire a few airplanes.
12. Build my own spaceship.
13. Build my own research satellite.
14. Visit the moon.
15. P vs. NP.
16. Climb Aconcagua.
17. Climb Mt. Denali.
18. Climb Mt. Everest.
19. Learn to fly a plane.
20. Visit Mt. Thor (Baffin island).
21. Sail to Ball's Pyramid from Sydney.
22. Visit Svalbard.
23. Directly observe the event horizon of the Milky Way central black hole.
24. Solve the mystery of baryon asymmetry.
25. Solve the mystery of dark energy and dark matter.
26. Crack FTL/time travel or prove them impossible.
27. Find extraterrestrial life.
28. Learn creative drawing.
29. Walk across the Canadian wilderness (~5000 km).
30. If there is a mystery related to human consciousness, solve it, if not, make it obvious for everone there is none.
31. See the day when religions basically are no more.
32. See the day when aging and all disease are cured.
33. See the Milky Way-Andromeda collision.
34. Visit a planet inhabited by estraterrestrial life.
35. Develop more meaningful social relationships.
36. Acquire a nice pacific island and build my own winter retreat there.
37. Acquire an underground missile base from the US and make it nice.
38. Acquire some weapons and explosives for fun and distribute them to my retreats all around the world.
39. Stockpile the retreats with supplies and build bunkers.
40. Visit Antarctica and Cape Horn area, Greenland, Siberia, India, China, New Zealand, Jordan, Africa...
41. Build an internationally successful company that manufactures useful hardware, solves a number of practical problems and employs a number of good people.
42. Make a game that tells an interesting story, teaches a few things and presents practical problems requiring decent problem solving skills.
43. Work for a while as national park ranger, chemist, philosopher, politician and as a neuroscientist.
44. Work for a while on genetic research and related biological issues.
45. Work for a while for NASA, nvidia, AI research, weapons research, some startups...
46. Live a few years in the wilderness and a monestary.
47. Try living in different cities around the world.
48. Get a cabin from Norway from some nice remote mountain slope next to a small lake with a small airstrip where I can fly from Finland with my own small plane.
49. Get a nice place from somewhere along the Californian cost, not too far from San Francisco, but in a not too densely populated location either.
50. Write a book that will stir up people and teach them some critical thinking.
* The word "prove" used in colloquial sense here.
 |
| Though I didn't like this particular turn of events in that particular episode as in my opinion while it is not possible to avoid all mistakes given the initial conditions, I never the less believe that losing is due to mistakes that under perfect knowledge and logic should not exist. Choose your mistakes wisely and you'll be fine. |
Unexamined life is not worth living is often taken to imply that rather than not being worth living some lives are simply missing something important. I would, however, argue that all lives are missing something important and on the other than that no single thing in any life is something so important that one should consider it essential. Most life has intrinsic value that is independent of its fullness.
It is often also said that the saying refers to one being able to say why things are important, right or wrong rather than simply insisting they are. However, this too is a bit arbitrary as in the end there never seems to be any why. We are what we are and want what we want, because that's the way we have come to be. Some goals are better served by some actions, but no action is right or wrong without reference to motivations which in end are arbitrary. Without such motivations we would not be humans, but rather simple machines simply waiting to do what we are told.
It is of course worthwhile to know how to influence other people by justifying actions and inactions for the betterment of humanity in general.